FX取引における主成分分析(PCA)の活用方法を解説します。本記事では以下の内容を取り上げます:
- PCAの基本概念と仕組み
- FX取引データへのPCA適用手順
- MT5でのPCA実装例:オシレーター分析
- PCAを用いたFX取引戦略の高度化と将来展望
複雑なFX市場データを単純化し、効果的な取引戦略を構築するためのPCAの可能性を探ります。

MQLでディープラーニングをするなら知っておくべきPCAを解説!!
主成分分析(PCA)とは:データ分析の強力なツール
主成分分析(PCA)は、多次元データを少数の重要な次元(主成分)に縮約する統計的手法です。FX市場のような複雑なシステムでは、多くの変数が相互に影響し合っています。PCAは、これらの変数間の関係を分析し、データの中で最も重要な傾向や特徴を見出すことができます。
PCAの基本概念と仕組み
PCAは、データの分散を最大化する新しい軸(主成分)を見つけることです。具体的には以下のステップで行われます:
- データの標準化:各変数のスケールを揃えます。
- 共分散行列の計算:変数間の関係を数値化します。
- 固有値と固有ベクトルの計算:データの主要な方向性を特定します。
- 主成分の選択:最も重要な情報を含む成分を選びます。
これらのステップにより、元のデータセットの主要な特徴を保持しながら、次元数を大幅に減らすことができます。

次元削減をしなくてもある程度は特徴量の重要度分析で不必要な特徴量の学習を避けてはくれるけど、PCAはそれ以上のメリットがあるのよね(‘Д’)
多重共線性の回避、学習の公理化、過学習の防止などなど!
パラメーターが多くなればなるほど必要になってくるよ
FX取引におけるPCAの活用方法
FX取引では、為替レート、経済指標、テクニカル指標など、多くの変数を考慮する必要があります。PCAを活用することで、以下のような利点が得られます:
- データの圧縮:多数の指標を少数の主成分に集約できます。
- ノイズの削減:市場の本質的な動きを捉えやすくなります。
- 隠れたパターンの発見:通常は見逃しがちな市場の構造を明らかにできます。
例えば、複数の通貨ペアの相関関係を分析する際に、PCAを使用すると、市場全体の動きを代表する少数の主成分を特定できます。これにより、より効率的なポートフォリオ管理や、リスク分析が可能になります。
PCAの実装手順:ステップバイステップガイド
PCAを実際のFX取引データに適用する手順を、詳しく見ていきましょう。
データの準備と標準化
まず、分析対象のデータを収集し、適切な形式に整理します。FX取引では、為替レート、各種経済指標、テクニカル指標などが対象となります。データの標準化は非常に重要なステップです。各変数のスケールが大きく異なる場合、結果が歪む可能性があるためです。
matrix Matrix = matrix_utiils.ReadCsv("bp data.csv");
pre_processing = new CPreprocessing(Matrix, NORM_STANDARDIZATION);標準化の一般的な方法は、各変数から平均を引き、標準偏差で割ることです。これにより、すべての変数が平均0、標準偏差1の分布になります。
共分散行列の計算
標準化されたデータから共分散行列を計算します。共分散行列は、各変数ペア間の関係を示す重要な情報を提供します。FX市場では、この段階で通貨ペア間の相関関係や、各経済指標がどのように相互に影響し合っているかを把握できます。
matrix Cova = Matrix.Cov(false);
Print("Covariances\n", Cova);固有値と固有ベクトルの導出
共分散行列から固有値と固有ベクトルを計算します。固有値は各主成分の重要度を示し、固有ベクトルは主成分の方向を示します。FX取引では、この段階で市場の主要な動きの方向性と、各要因の重要度を理解することができます。
if (!Cova.Eig(component_matrix, eigen_vectors))
Print("Failed to get the Component matrix matrix & Eigen vectors");主成分の選択と解釈
固有値の大きさに基づいて、最も重要な主成分を選択します。一般的に、累積寄与率が80%〜90%に達するまでの主成分を選びます。
選択された主成分の解釈は、FX取引戦略の構築において非常に重要です。例えば、第一主成分が全体的な市場のトレンドを表し、第二主成分が特定の経済セクターの影響を示している可能性があります。これらの洞察を基に取引戦略を立てることができます。

Pythonでやればよくね?って思うじゃない?
バックテスト時にPython使えないからPCAはMQLでやるのだ(‘Д’)
MT5でのPCA活用例:オシレーター分析
MT5は、多くのFXトレーダーに愛用されているプラットフォームです。MT5でPCAを活用する具体例として、複数のオシレーターを分析するケースを見てみましょう。
複数のオシレーターを使用したデータセットの作成
まず、以下のようなオシレーターを選択し、データセットを作成します:
- RSI(相対力指数)
- ストキャスティクス
- MACD(移動平均収束拡散法)
- CCI(商品チャネル指数)
- ウィリアムズ%R
handles[0] = iATR(Symbol(),PERIOD_CURRENT, period);
handles[1] = iBearsPower(Symbol(), PERIOD_CURRENT, period);
handles[2] = iMACD(Symbol(),PERIOD_CURRENT,12, 26,9,PRICE_CLOSE);
handles[3] = iChaikin(Symbol(), PERIOD_CURRENT,12,26,MODE_SMMA,VOLUME_TICK);
handles[4] = iCCI(Symbol(),PERIOD_CURRENT,period, PRICE_CLOSE);
handles[5] = iDeMarker(Symbol(),PERIOD_CURRENT,period);
handles[6] = iForce(Symbol(),PERIOD_CURRENT,period,MODE_EMA,VOLUME_TICK);
handles[7] = iMomentum(Symbol(),PERIOD_CURRENT,period, PRICE_CLOSE);
handles[8] = iRSI(Symbol(),PERIOD_CURRENT,period,PRICE_CLOSE);
handles[9] = iWPR(Symbol(),PERIOD_CURRENT,period);
for (int i=0; i<10; i++)
{
matrix_utiils.CopyBufferVector(handles[i],0,0,bars,buff_v);
ind_Matrix.Col(buff_v, i);
}これらのオシレーターは、それぞれ異なる側面から市場の動きを捉えています。しかし、同時に多くの情報が重複している可能性もあります。

非常に重要な記事、ぜひ本家記事も見てね!
PCAを用いたオシレーターデータの次元削減
収集したオシレーターデータにPCAを適用します。この過程で、オシレーター間の相関関係が明らかになり、冗長な情報を排除できます。例えば、RSIとストキャスティクスは類似した情報を提供している可能性が高いですが、PCAはこれらの共通要素を1つの主成分として抽出します。
pca = new Cpca(ind_Matrix);
matrix pca_matrix = pca.ExtractComponents(ENUM_CRITERION);結果の可視化と解釈
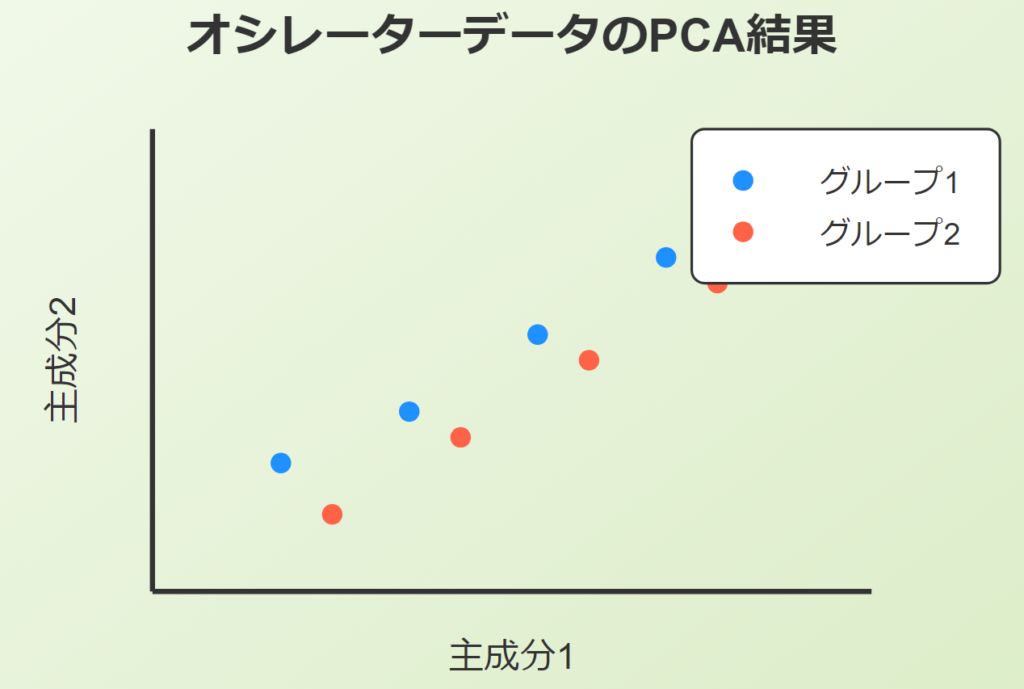
PCAの結果を視覚化することで、オシレーター間の関係性やその重要度をより直感的に理解できます。例えば、散布図を使用して、各オシレーターが主成分にどのように寄与しているかを表示できます。
plt.ScatterCurvePlotsMatrix("pca's ",pca_matrix,"var","PCA");この分析により、例えば「第一主成分はトレンドの強さを、第二主成分は市場のモメンタムを表している」といった解釈が可能になります。これらの洞察を基に、より効率的な取引戦略を構築できます。
PCAの利点と注意点:FX取引への適用
PCAはFX取引に多くの利点をもたらしますが、同時にいくつかの注意点もあります。
データ圧縮とノイズ削減のメリット
PCAの最大の利点は、複雑なデータセットを簡略化できることです。FX市場では、多くの指標やシグナルが存在しますが、それらの多くは相関関係にあり、実質的に同じ情報を提供している場合があります。PCAを使用することで、本質的な市場動向に焦点を当てることができます。
また、PCAはデータのノイズを減らす効果もあります。FX市場では短期的な価格変動が頻繁に起こりますが、これらの多くは長期的なトレンドとは無関係なノイズである可能性があります。
PCAは主要な変動要因を抽出することで、このようなノイズの影響を軽減し、より安定した分析結果を提供します。
情報損失のリスクと解釈の難しさ
一方で、PCAには注意すべき点もあります。最も重要なのは、情報損失のリスクです。PCAは本質的にデータを圧縮する手法であるため、一部の情報が失われる可能性があります。特に、稀に発生する重要なイベント(例:急激な市場変動)に関する情報が、主成分に十分に反映されない可能性があります。
また、主成分の解釈が難しい場合があります。PCAは数学的に導出された成分を生成するため、それらが実際の経済的または市場的な意味を持つとは限りません。これらの抽象的な成分を取引戦略にどのように組み込むかを検討する必要があります。
まとめ:PCAを活用したFX取引戦略の高度化
主成分分析(PCA)は、FX取引における複雑なデータ分析を大幅に簡素化し、効率化する強力なツールです。本記事で紹介したように、PCAを活用することで、多数の指標や変数から本質的な市場動向を抽出し、より洗練された取引戦略を構築することが可能になります。
PCAの実践的応用方法
- 市場構造の理解:PCAを使用して、様々な通貨ペアや経済指標間の関係性を明らかにし、市場の全体的な構造をより深く理解します。
- ポートフォリオ最適化:主成分を基にリスク分散を行い、より効率的なポートフォリオ構築が可能になります。
- シグナル生成:PCAで抽出された主要な市場動向を基に、より信頼性の高い取引シグナルを生成できます。
- リスク管理:主成分を通じて市場の主要なリスク要因を特定し、より効果的なリスク管理戦略を立てることができます。
今後の展望と課題
PCAはFX取引の分析ツールとして大きな可能性を秘めていますが、その効果的な活用にはいくつかの課題も存在します。
- リアルタイムデータへの適用:市場環境は常に変化しているため、PCAをリアルタイムデータに適用する手法の開発が重要になります。
- 非線形関係の扱い:PCAは基本的に線形の関係を前提としているため、非線形の市場動向を捉えるには追加の手法が必要になる可能性があります。
- 解釈可能性の向上:主成分の意味をより直感的に理解し、実際の取引戦略に組み込むための手法の開発が求められます。
- 他の機械学習手法との統合:PCAを他の高度な機械学習アルゴリズムと組み合わせることで、さらに洗練された分析が可能になるかもしれません。
FX取引において、PCAは複雑なデータを単純化し、重要な洞察を得るための強力なツールです。今後、AI技術の発展とともに、PCAを含むデータ分析手法はさらに進化し、FX取引の世界に革新をもたらすことが期待されます。
オンラインコミュニティ
こちらのコミュニティで、AIや機械学習をトレードに活かすために日々探求しています。
興味のある方は覗いてみてください。
参考記事