決定木アルゴリズムを使った取引に興味はありませんか?この記事を読むと、以下のことが学べます:
- EAで決定木モデルを作る方法
- 市場データを分析して、正確な取引のタイミングを見つける技術
- モデルが現実の市場でも通用するようにする方法
- 決定木の長所を生かした、分かりやすく調整しやすい取引システムの作り方
これらの知識を使えば、あなたの取引方法を改善し、市場でより良い結果を出せるかもしれません。初心者からベテランまで、決定木を使って新しい取引方法を見つけましょう。

これは、EAで決定木の機械学習ができちゃう有料級のライブラリだよ
決定木について
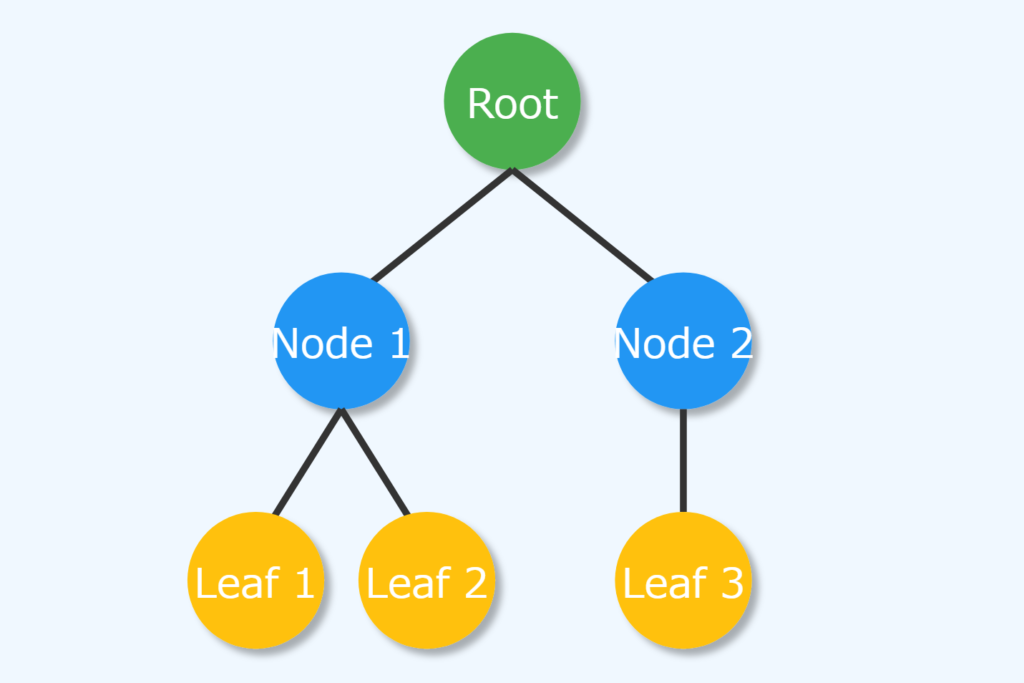
決定木は機械学習の基本的な方法の一つで、データを分類したり数値を予測したりするのに使います。木の形をしていて、データを分けて予測や判断をします。人間にも理解しやすく、どうやって判断したかを見ることができるのが特徴です。
ノードについて
決定木には主に2種類のノードがあります:内部ノードと葉ノード。内部ノードはデータの特徴に基づいて判断し、データをさらに小さなグループに分けます。各内部ノードでは、特定の特徴について「はい」か「いいえ」の質問をし、答えによってデータを左右の子ノードに振り分けます。
葉ノードは木の終わりを表し、最終的な予測や分類を示します。例えば、分類問題では葉ノードがグループの名前を、数値予測問題では具体的な数字を予測します。
ノードの構成要素
class Node
{
public:
// for decision node
uint feature_index;
double threshold;
double info_gain;
// for leaf node
double leaf_value;
Node *left_child; //left child Node
Node *right_child; //right child Node
Node() : left_child(NULL), right_child(NULL) {} // default constructor
Node(uint feature_index_, double threshold_=NULL, Node *left_=NULL, Node *right_=NULL, double info_gain_=NULL, double value_=NULL)
: left_child(left_), right_child(right_)
{
this.feature_index = feature_index_;
this.threshold = threshold_;
this.info_gain = info_gain_;
this.value = value_;
}
void Print()
{
printf("feature_index: %d \nthreshold: %f \ninfo_gain: %f \nleaf_value: %f",feature_index,threshold, info_gain, value);
}
};各ノードには以下のような情報が入っています:
- テスト条件:内部ノードでデータを分ける基準(例:「年齢が30歳より上か」)
- 特徴と基準値:分けるのに使う特徴とその基準値
- グループの名前や数値:葉ノードでの予測結果
- 子ノード:内部ノードが持つ、次の判断段階を表すノード
これらが組み合わさって、決定木は複雑な判断の過程を表現できます。
決定木の種類
主な決定木の方法には以下のようなものがあります:
- CART (Classification and Regression Trees)
- 2つに分かれる木を作り、分類と数値予測の両方に使える
- データの不純さや平均二乗誤差を使って分け方を決める
- ID3 (Iterative Dichotomiser 3)
- 主に分類問題に使う
- 情報の増加量を使って分け方を決める
- カテゴリ変数を扱うのが得意
- C4.5
- ID3を改良したもの
- 連続的な数値も扱える
- 情報増加率を使って、多くの値を持つ属性に偏らないようにする
これらの方法はそれぞれ特徴が違うので、問題に合わせて適切なものを選ぶことが大切です。
ID3 (Iterative Dichotomiser 3)
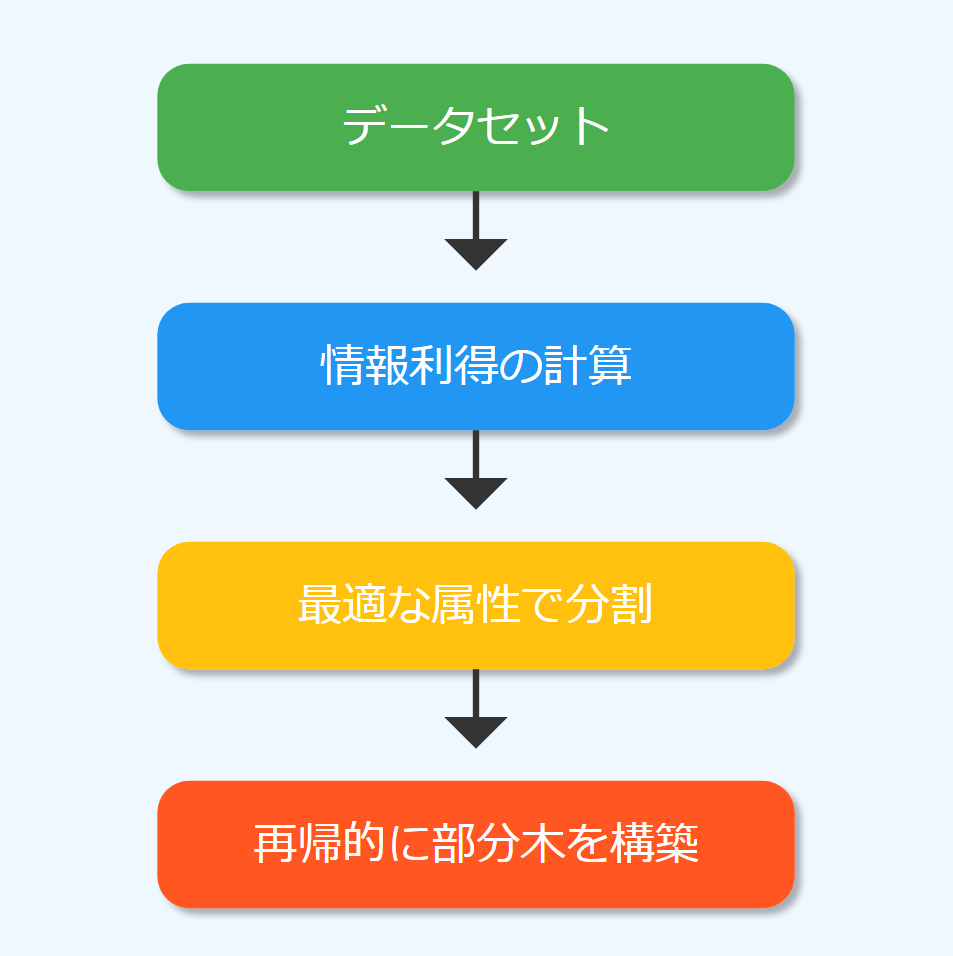
ID3は決定木の方法の中でも特に重要です。この方法は情報理論の考え方を使って、各ノードでのデータの分け方を決めます。
ID3の核心は情報利得という考え方です。情報利得は、ある特徴を使ってデータを分けたときに、どれだけ情報が増えるかを測ります。具体的には、分ける前と後でのデータの乱雑さ(エントロピー)の差として計算します。
エントロピーの計算式:
H(S) = -Σ(p_i * log2(p_i))
ここで、p_iは各クラスの確率を表します。
情報利得の計算式:
IG(S, A) = H(S) – Σ((|S_v| / |S|) * H(S_v))
ここで、Sはデータセット、Aは属性、S_vは属性Aの値vを持つサブセットです。
ID3の方法は、各段階で最も情報利得が大きくなる特徴を選んでデータを分けます。これにより、できるだけ少ない質問で最も効率よくデータを分類できます。
double CDecisionTree::entropy(vector &y)
{
vector class_labels = matrix_utils.Unique_count(y);
vector p_cls = class_labels / double(y.Size());
vector entropy = (-1 * p_cls) * log2(p_cls);
return entropy.Sum();
}
double CDecisionTree::information_gain(vector &parent, vector &left_child, vector &right_child)
{
double weight_left = left_child.Size() / (double)parent.Size(),
weight_right = right_child.Size() / (double)parent.Size();
double gain =0;
switch(m_mode)
{
case MODE_GINI:
gain = gini_index(parent) - ( (weight_left*gini_index(left_child)) + (weight_right*gini_index(right_child)) );
break;
case MODE_ENTROPY:
gain = entropy(parent) - ( (weight_left*entropy(left_child)) + (weight_right*entropy(right_child)) );
break;
}
return gain;
}
FXの相場はノイズが多いから、エントリピーを推奨するよ
決定木の作り方
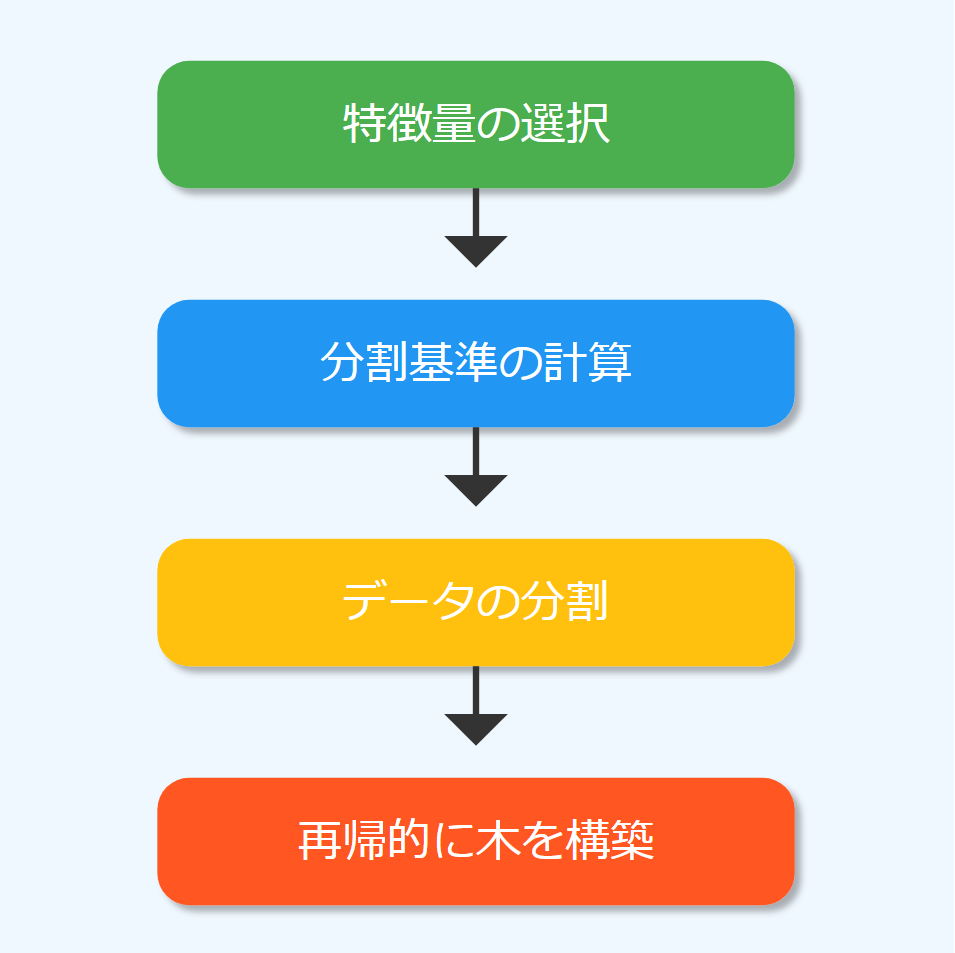
決定木を作る過程は、同じ手順を繰り返す簡潔な方法です。以下にその詳細を説明します。
分割基準
決定木を作る上で最も大切なのは、各ノードでどの特徴を使って、どのようにデータを分けるかを決めることです。主な基準には以下のようなものがあります:
- 情報利得(ID3で使用): 前述の通り、エントロピーの減少量を測ります。
- ジニ不純度(CARTで使用): データの分類の純度を測ります。
- 分散の減少(数値予測問題で使用): 分ける前と後での数値のばらつきの減少量を測ります。
これらの指標を使って、各ノードで最適な分け方を決めます。
split_info CDecisionTree::get_best_split(matrix &data, uint num_features)
{
double max_info_gain = -DBL_MAX;
vector feature_values = {};
vector left_v={}, right_v={}, y_v={};
//---
split_info best_split;
split_info split;
for (uint i=0; i<num_features; i++)
{
feature_values = data.Col(i);
vector possible_thresholds = matrix_utils.Unique(feature_values); //Find unique values in the feature, representing possible thresholds for splitting.
for (uint j=0; j<possible_thresholds.Size(); j++)
{
split = this.split_data(data, i, possible_thresholds[j]);
if (split.dataset_left.Rows()>0 && split.dataset_right.Rows() > 0)
{
y_v = data.Col(data.Cols()-1);
right_v = split.dataset_right.Col(split.dataset_right.Cols()-1);
left_v = split.dataset_left.Col(split.dataset_left.Cols()-1);
double curr_info_gain = this.information_gain(y_v, left_v, right_v);
if (curr_info_gain > max_info_gain) // Check if the current information gain is greater than the maximum observed so far.
{
#ifdef DEBUG_MODE
printf("split left: [%dx%d] split right: [%dx%d] curr_info_gain: %f max_info_gain: %f",split.dataset_left.Rows(),split.dataset_left.Cols(),split.dataset_right.Rows(),split.dataset_right.Cols(),curr_info_gain,max_info_gain);
#endif
best_split.feature_index = i;
best_split.threshold = possible_thresholds[j];
best_split.dataset_left = split.dataset_left;
best_split.dataset_right = split.dataset_right;
best_split.info_gain = curr_info_gain;
max_info_gain = curr_info_gain;
}
}
}
}
return best_split;
}木を作る
決定木を作る過程は以下のようになります:
- 根のノードから始め、すべての学習データを含めます。
- 使える全ての特徴に対して分け方の基準(例:情報利得)を計算します。
- 最も高いスコアを持つ特徴を選び、その特徴でデータを分けます。
- 分けたデータに対して、子ノードを作ります。
- 各子ノードに対して、2-4の手順を繰り返します。
- 以下のいずれかの条件に達したら、葉ノードを作って終了します:
- ノード内の全てのデータが同じグループに属する
- 使える特徴がなくなった
- 木の深さが最大値に達した
- ノード内のデータ数が最小値を下回った
Node *CDecisionTree::build_tree(matrix &data, uint curr_depth=0)
{
matrix X;
vector Y;
matrix_utils.XandYSplitMatrices(data,X,Y); //Split the input matrix into feature matrix X and target vector Y.
ulong samples = X.Rows(), features = X.Cols(); //Get the number of samples and features in the dataset.
Node *node= NULL; // Initialize node pointer
if (samples >= m_min_samples_split && curr_depth<=m_max_depth)
{
split_info best_split = this.get_best_split(data, (uint)features);
#ifdef DEBUG_MODE
Print("best_split left: [",best_split.dataset_left.Rows(),"x",best_split.dataset_left.Cols(),"]\nbest_split right: [",best_split.dataset_right.Rows(),"x",best_split.dataset_right.Cols(),"]\nfeature_index: ",best_split.feature_index,"\nInfo gain: ",best_split.info_gain,"\nThreshold: ",best_split.threshold);
#endif
if (best_split.info_gain > 0)
{
Node *left_child = this.build_tree(best_split.dataset_left, curr_depth+1);
Node *right_child = this.build_tree(best_split.dataset_right, curr_depth+1);
node = new Node(best_split.feature_index,best_split.threshold,left_child,right_child,best_split.info_gain);
return node;
}
}
node = new Node();
node.leaf_value = this.calculate_leaf_value(Y);
return node;
}この過程を通じて、データの構造を反映した決定木ができあがります。

予測には少々時間がかかるから、バックテスト中に学習は非現実的もしくは効率を考えなきゃいかん
取引における決定木AI
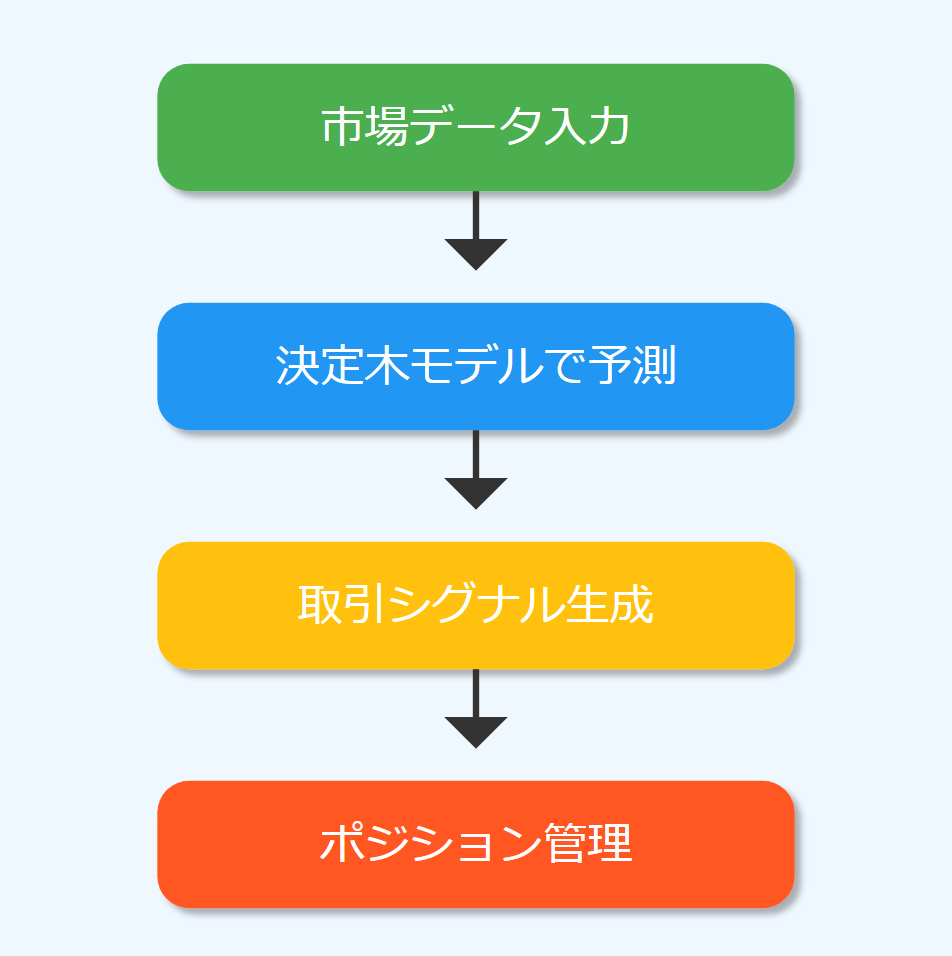
決定木は、分かりやすさと柔軟性から、金融取引の分野でも広く使われています。MQL5を使った取引システムに決定木を組み込むことで、より高度な取引方法を実現できる可能性があります。

初心者にはまず扱いやすい決定木がおすすめ!
解決できる問題
取引で典型的に解決したい問題として、次のような例が挙げられます:
- 次の価格変動が上がるか下がるかの予測
- 特定の時間内で大きな価格変動が起きるかどうかの予測
- 最適な取引開始と終了のタイミングの特定
これらの問題に対して、決定木は過去の市場データと指標を使って、パターンを学習し予測を行います。
データ構造体
MQL5で決定木モデルを作る際、以下のようなデータの構造を使うと効果的です:
struct data{
vector stoch_buff,
signal_buff,
rsi_buff,
target;
} data_struct;この構造体は、ローソク足データに加えて、一般的な指標を含んでいます。予測対象は、次の価格変動の方向を表します。
データの収集、決定木の学習とテスト
MQL5で決定木モデルを学習させる過程は以下のようになります:
- ヒストリカルデータの収集
- データの前処理
- 訓練データとテストデータの分割
- 決定木モデルの訓練
- モデルの評価
リアルタイム予測
学習させたモデルを使ってリアルタイムで取引のタイミングを決める方法は以下の通りです:
- 現在の市場データを取得する
- データを決定木モデルの入力形式に変換する
- モデルを使って予測を行う
- 予測結果に基づいて取引のタイミングを決める
int desisionTreeSignal()
{
//--- Copy the current bar information only
data_struct.rsi_buff.CopyIndicatorBuffer(rsi_handle, 0, 0, 1);
data_struct.stoch_buff.CopyIndicatorBuffer(stoch_handle, 0, 0, 1);
data_struct.signal_buff.CopyIndicatorBuffer(stoch_handle, 1, 0, 1);
x_vars[0] = data_struct.rsi_buff[0];
x_vars[1] = data_struct.stoch_buff[0];
x_vars[2] = data_struct.signal_buff[0];
return int(decision_tree.predict(x_vars));
}
void OnTick()
{
//---
if (!train_once) // You want to train once during EA lifetime
TrainTree();
train_once = true;
if (isnewBar(PERIOD_CURRENT)) // We want to trade on the bar opening
{
int signal = desisionTreeSignal();
double min_lot = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
SymbolInfoTick(Symbol(), ticks);
if (signal == -1)
{
if (!PosExists(MAGICNUMBER, POSITION_TYPE_SELL)) // If a sell trade doesnt exist
m_trade.Sell(min_lot, Symbol(), ticks.bid, ticks.bid+stoploss*Point(), ticks.bid - takeprofit*Point());
}
else
{
if (!PosExists(MAGICNUMBER, POSITION_TYPE_BUY)) // If a buy trade doesnt exist
m_trade.Buy(min_lot, Symbol(), ticks.ask, ticks.ask-stoploss*Point(), ticks.ask + takeprofit*Point());
}
}
}この関数を定期的に呼び出すことで、市場の変化に応じたリアルタイムの取引シグナルを得ることができます。
取引における決定木に関するFAQ
- Q決定木は他の機械学習の方法と比べてどうですか?
- A
決定木は分かりやすく、データの前処理が簡単という利点がありますが、他の方法と比べて精度が低いことがあります。
- Q決定木で時系列データを扱う際の注意点は?
- A
時系列データの場合、データの順序が重要なので、適切な特徴量の作成や、時間の要素を考慮したモデルの設計が必要です。
- Q決定木の過学習を防ぐにはどうすればいいですか?
- A
以下の方法が効果的です:
- 最大深さの制限
- 最小サンプル数の設定
- プルーニング(事後の枝刈り)
- クロスバリデーションの使用
- QMQL5で決定木を実装する際のパフォーマンスの注意点は?
- A
決定木の予測は高速ですが、学習には時間がかかる場合があります。リアルタイムでの再学習は避け、定期的(例:日次)に学習を行い、モデルを更新することをお勧めします。
決定木のメリット・デメリット

メリット
- 解釈可能性:決定木の構造は人間が理解しやすく、モデルの決定プロセスを追跡できます。
- 非線形関係の取り扱い:複雑な非線形関係も表現できます。
- 特徴量の重要度:木の構造から各特徴量の重要度を容易に算出できます。
- データの準備が簡単:数値の調整や正規化が不要で、欠けているデータにも強いです。
- 様々な種類のデータを扱える:数値もカテゴリも同時に扱えます。
デメリット
- 過学習:深い木は訓練データに過剰に適合しやすく、汎化性能が低下する可能性があります。
- 不安定性:データの小さな変化で木の構造が大きく変わることがあります。
- 最適解の保証がない:局所最適解に陥る可能性があります。
- 軸平行な決定境界:斜めの決定境界を表現するのが苦手です。
- データの偏りに弱い:多数派のデータに偏った予測をしやすいです。

デメリットは機械学習全般に言えることでもある
対策はあるから問題なし
まとめ
決定木は分かりやすく強力な機械学習の方法で、MQL5を使った取引システムに簡単に組み込めます。その分かりやすさと調整のしやすさは、取引方法の開発と改善に大きな価値をもたらします。ただし、単独の決定木には限界もあるので、より高度な方法(ランダムフォレストやグラディエントブースティングなど)の使用も検討する価値があります。
決定木を上手に使うには、適切な特徴の選び方、パラメータの調整、そして現実のデータにも対応できるようにする技術が重要です。
オンラインコミュニティ
こちらのコミュニティで、AIや機械学習をトレードに活かすために日々探求しています。
興味のある方は覗いてみてください。
参考記事:


サンプルのライブラリが更新されてることもあるから、
著者のGithubから新しいライブラリをDLすることをお勧めします!
