為替レートの予測では、日時や季節に関わる特徴量(Hour=時刻、Month=月、DayOfWeek=曜日、DayOfYear=年の日数など)をモデルに組み込むことが多いです。
これらの時間情報をどうエンコードするかはモデルの性能に影響します。本記事ではサイクリックエンコーディング(循環エンコーディング)の有用性について、CatBoostのような決定木ベースモデルでの扱い方や、金融時系列データでの効果、過学習への影響、そして実務上の事例を初心者向けに解説します。
時系列特徴量の課題:「循環する」時間データ
時間に関する特徴量(時刻や月など)は循環的な性質を持ちます。例えば「23時」と「0時」は時計で見ると1時間しか離れていませんが、数値上は23と0で大きく離れており、そのまま数値特徴量として扱うと端と端が遠いものとして認識されてしまいます。同様に、12月(12)と1月(1)も本来連続した月ですが、数値では12と1で離れているため、この関係をモデルが誤解する可能性がありますmdpi.com。これは曜日についても言え、日曜と月曜が隣り合う曜日であることを数値だけでは表現できません。

こうした問題に対処するために、従来いくつかの方法があります:
- 単純な数値(非サイクリック): 時間をそのまま整数値(0~23の時刻や1~12の月など)で入力する方法。連続性を多少持たせますが、先述のように周期の端同士が遠くなる欠点があります。また「12月 > 1月」のような大小関係があるとモデルが誤解する恐れもあります。
- ワンホットエンコーディング: 24時間なら24次元のベクトルで特定の時刻だけ1、それ以外0とする方法です。曜日や月も同様に各カテゴリをビットで表現できます。周期の端と端が疎遠になる問題は避けられますが、特徴量の次元が増えすぎたり、各カテゴリが互いに等距離とみなされてしまい近さの概念は表現されません。またデータが少ないカテゴリでは過学習のリスクもあります。
- サイクリックエンコーディング: サイン・コサイン関数で角度に変換し、2つの値で円周上の座標として表現する方法です。これにより23時と0時はほぼ同じ(x,y)に近い値となり、周期のつながりを特徴量が表現しますmdpi.com。月や曜日についても同様です。

上図のように、サイクリックエンコーディングでは時間の周期を円として表現するため、周期の端同士が近い位置に配置されます。これによりモデルは「翌日・翌月に周回する繰り返しパターン」を学習しやすくなります。実際、エネルギー需要予測の研究では、時間をサイン・コサインでエンコードすることで周期的パターンを的確に捉え、ワンホットよりも汎化性能が向上したと報告されていますmdpi.com。
サイクリック vs 非サイクリック:どちらが有効か?
それでは、サイクリックエンコーディングは常に有効なのでしょうか?結論としては、「データとモデルによる」というのが実務での知見です。いくつか比較ポイントを見てみましょう。
- 近接する時刻・日時を学習できるか: サイクリックエンコーディングは上述の通り、連続する時間同士を近い値で表現できます。例えば、モデルに月を数値12と1で与えた場合、12月と1月の関連性を捉えにくいですが、サイン・コサインなら近接したベクトルになりますmdpi.com。Kaggleの議論でも「12月(12)と1月(1)をそのままでは年末年始の連続性を誤解する可能性があるが、サイクリック変換であれば問題を緩和できる」と指摘されています(※)developer.nvidia.com。一方、ワンホットでは12月と1月は全く別の次元で表現され距離の概念がないため、モデルに「隣同士」と教えることは難しいです。この点でサイクリック>ワンホット>単純数値といった優位性があると言えます。

- 特徴量の数・情報量: ワンホットはカテゴリ数だけ次元が増えます。例えば日付を「月・日」でワンホットにすると最大31+12=43次元にもなります。一方サイクリックなら2次元に圧縮できます。少ない次元で周期情報を保持できるのはサイクリックの利点ですmdpi.com。ただし、サイクリックの2次元だけでは表現しきれない非対称な影響(例:特定の曜日だけ特異な効果)は、追加の特徴量が無いとモデルが表現しにくい場合があります。この場合はサイクリックに加えて「週末フラグ」「年末年始フラグ」のような補助的なワンホット特徴を入れる手もありますshrmtmt.medium.com。

- モデルが捉えやすいか(線形 vs 非線形): サイクリックエンコーディングはあらかじめ非線形な変換を施しており、線形モデルでも周期パターンを表現できます。実際、線形回帰モデルに日周期のsin, cos特徴を入れると季節変動をかなり滑らかにフィッティングできますdeveloper.nvidia.com。一方、単純な数値特徴だと線形モデルでは周期性を表現しにくく、ワンホットでは線形モデルでも対応できますが前述の通り次元増加の問題があります。ニューラルネットなど非線形性の高いモデルは、理論的には数値入力からでも周期パターンを学習可能ですが、そのためには十分な複雑さやデータ量が必要です。したがって、手軽に周期情報を与える意味でサイクリック変換は有効です。

以上の点から、線形モデルやディープラーニングではサイクリックエンコーディングが広く推奨されています。一方で決定木系モデルの場合は少し事情が異なります。次のセクションで詳しく見てみましょう。
CatBoostなど決定木モデルでの扱い
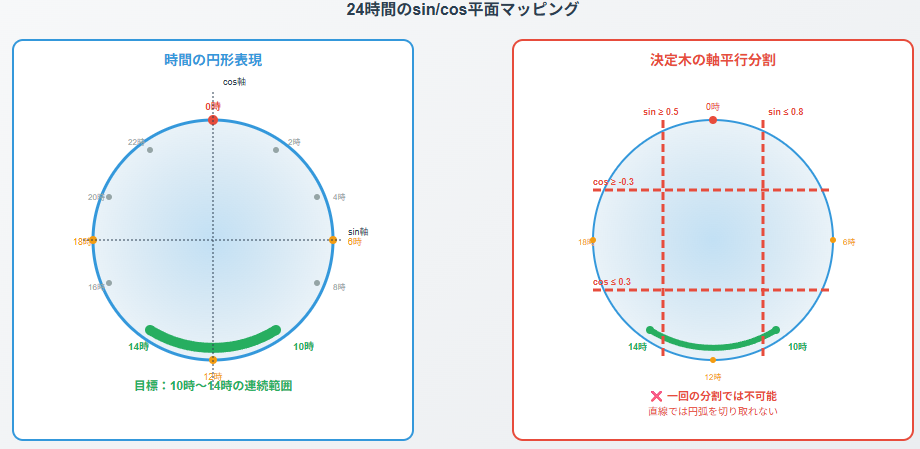
CatBoostやXGBoost、Random Forestといった決定木ベースのモデルは、基本的に単一特徴量に対してしきい値を切るという形でデータ分割を行います。このため、サイクリックエンコーディングで得られる「sin列」と「cos$列」の2つの特徴を同時に考慮することができません。直感的には、モデルにとってはsinとcosは別々の軸であり、本来はそれらが組み合わさって一つの円状座標を成すのに、木は個別にしきい値を作って分割するためうまく周期を切り取れないケースがありますstackoverflow.com。

例えば、24時間をsin, cosの平面上にマッピングすると円になりますが、決定木は縦横の軸に平行な境界でしかデータを区切れません。このため、一回の分割では円を直線で切ることになり、「10時~14時」といった連続した時間範囲を一発で表現するのが難しく、どうしても複数回の分割が必要になります。CatBoost開発者のやり取りでも、サイン・コサイン2変数にした場合とカテゴリー変数のまま扱った場合で大差ないことが多く、どちらが良いかはデータ次第とされています。実際、とあるユーザは時刻をサイン・コサインに変換してCatBoostに入力しても精度向上しなかったと報告していますgithub.com(むしろCatBoostでは時刻をカテゴリ型として扱ったほうがシンプルだったとの声もあります)。一般的な勧めとして、CatBoostでは時間をカテゴリ扱い(例えば曜日や月をカテゴリ特徴としてモデルに渡す)しても良く、CatBoostはそれを自動的に良い形でエンコード(ターゲットエンコーディングのような効果)してくれるため、無理に数値変換しなくてもよいという見解もありますarxiv.org。
もっとも、サイクリックエンコーディングが決定木で全く無意味かと言うとそうではありません。小規模な検証ではありますが、CatBoostに対し「時刻そのもの」を入力した場合と「sin, cos」を入力した場合で、後者のほうがなめらかに周期パターンを近似できたという結果もあります。これは、sin,cosで変換したことで値の連続性が改善され、木の分割による段差的な予測が減った可能性があります。実際その検証では、時間をそのまま入れた場合CatBoostの木の深さがあまり深くならず荒いステップ状の予測になったのに対し、$\sin,\cos$入力ではより深い木や多数のブーストステップを重ね、原関数(正弦波)に近い予測曲線を描けたと報告されていますstats.stackexchange.com。つまり、サイクリック特徴があれば決定木でも工夫次第で周期的な境界を細かく刻めるとも解釈できます。

サイン・コサイン2変数にした場合とカテゴリー変数のまま扱った場合で大差ないことが多い。どちらが良いかはデータ次第である。

時刻をsin・cosに変換してCatBoostに入力しても精度向上しなかった。むしろベースラインより悪化。

CatBoostでは時刻をカテゴリ型として扱った方がシンプルで効果的だった。実装も保守も楽。
以上をまとめると、CatBoostなどの決定木モデルでは:
- そのまま数値で時刻や月を与えても、木はしきい値条件でうまく周期を分割できる場合があります。ただし、0/23時のようなケースは2回の分割が必要になるなど、モデル任せにすると学習が難しい部分もある。

- カテゴリ特徴として与えると、CatBoostの場合は内部で頻度やターゲット統計量を使ったエンコーディングを行うため、暦の各値(曜日や月)の影響を自動で捉えやすくなりますarxiv.org。この方法では特にサイクリック変換は不要で、月=12と月=1が隣かどうかはモデル次第ですが、必要なら木が「月が12または1なら…」といった分割をすることも可能です。


Onnxではすべての特徴量をFloatで入力することになるから、カテゴリカルかどうかの指定は不要。Onnxでは②は①そのまま数値と同意になるよ(‘Д’)
- サイクリック特徴として与える場合、モデルが2変数を組み合わせて理解するのは簡単ではありませんが、うまく機能すれば連続的な周期パターンを表現しやすくなる利点もありますstats.stackexchange.com。一方で、木は本来ステップ関数的な表現をするので、サイクリックにしても完全な連続にはならない(むしろ中途半端に対称な領域区切りになる)点には注意が必要ですgithub.com。

結論として、CatBoostで時系列の周期特徴を扱う際は、まずはシンプルにカテゴリ型で投入して様子を見ることが多いです。それで不足を感じたり、モデルが端と端を繋ぐのに苦労していそうな場合にサイクリック特徴を追加してみる、というアプローチも考えられます。実務的には両方試して交差検証で比較し、より汎化性能が高い方を採用するのが安全策と言えるでしょうgithub.com。
金融時系列(為替など)での効果と留意点
金融データには日周期・週周期・年周期のパターンが存在すると言われます。例えば為替市場では時間帯による出来高や変動性の違い(ロンドン市場やNY市場の開閉時間に対応した動き)、週の中では月曜朝や金曜夕方の特殊な動き、季節的には年度末や長期休暇シーズンのトレンド変化など、いくつかの周期的要因が指摘されます。このような要因をモデルに織り込むには、適切な特徴量エンコーディングが重要です。
サイクリックエンコーディングは、これら周期要因をなめらかにモデルに伝える手段として有効です。過去のコンペ事例でも、時刻や曜日をサイン・コサイン特徴に変換することで**「週末明け」と「週末直前」のパターンを学習させやすくした例があります(例えば「23時と0時が連続している」ことをモデルが誤って無視しないように工夫developer.nvidia.com)。Kaggleのタイムシリーズ系競技でも、多くの上位チームが時間特徴のサイクリック変換を採用しています。実際、LightGBMやCatBoostといったモデルで時系列予測を行う際は、ラグ特徴や移動統計量と並んで時間のsin/cos変換**が定番の特徴エンジニアリングになっていますnimasarang.com。

しかし金融時系列ならではの注意点もあります:
- 過学習のリスク: 周期的な傾向が毎回同じとは限らず、年によって違う動きをすることもあります。サイクリックエンコーディングは「毎年(毎週)同じサイクルで動く」ことを前提に特徴を作るため、もしデータの中で偶然起きた単発の現象を周期と誤認すると過学習につながります。例えば年に一度のイベント(大きな政策発表など)が特定の日に集中して起きたとします。それをDayOfYearのsin/cosが捉えてしまうと、「この日は毎年特別」という誤学習をする恐れがあります。特に学習期間が短く各値のサイクルを十分経験していない場合(日足データ2年分で365日のsin/cosを使うなど)は注意が必要です。サイクリックエンコーディング自体は過学習を直接招くものではありませんが、365通りのユニークな組合せを2変数で表現できてしまうため、モデルがそれを覚え込めば実質的に一日ごとのダミー変数と同じくらい柔軟に当てはめてしまう可能性があります。

- 急峻なパターンへの対処: 金融市場では土日で市場がクローズする関係上、月曜と日曜の相場には大きなギャップ(窓開け)が生じたり、特定の曜日だけ出来高が跳ねるといった急峻(ディスコンティニュアス)な現象が見られます。このような非連続な跳ねをサイン・コサインだけで表現するのは難しく、モデルに大きな隠れ層(複雑さ)が必要になる場合があります。そのため、実務上はサイクリックエンコーディングに加えて、「金曜=1他=0」のような曜日のワンホット特徴や「市場営業日フラグ」といった補助特徴も組み合わせることがあります。Shiro Matsumoto氏のまとめによれば、人間の行動に起因する社会経済的なデータでは、サイクルだけでは表現しづらいピンポイントの効果があるためワンホットと併用する方が効率的で頑健な場合も多いとされています。ただしワンホットを使う際は各カテゴリ(曜日など)に十分なサンプルがあるか確認し、不均衡だと逆に過学習する点に注意が必要ですshrmtmt.medium.com。

- モデル選択との関係: 前述のように、もし為替予測でCatBoostのような決定木モデルを使うなら、サイクリックエンコーディングは効果が限定的かもしれませんstackoverflow.com。一方、ディープラーニング(LSTMやTransformerなど)を使う場合や、線形回帰・SVMといったモデルを使う場合は、サイクリックエンコーディングが時間情報を伝える標準手法と言えますarxiv.org。実際、ある研究では決定木系モデルには日・月・曜日をそのまま整数で与え、ニューラルネット系モデルにはsin/cosを使ったというアプローチが取られていますarxiv.org。モデルの種類によって適切なエンコーディングを選ぶことも重要です。

実務・コンペでの活用例
- 機械学習コンペ(Kaggle等): 需要予測や売上予測など、日時情報がカギとなる課題では、多くの上位解法がサイクリックエンコーディングを採用していますnimasarang.com。例えばあるKaggleコンペの解法では「時間(時刻)のwrap-around(23時と0時が繋がる現象)を捉えるためにsin・cosを追加した」と言及されています(Hours 23 and 0 are adjacent の考慮)。また別の分析ノートでは「サイクリック特徴によってモデルが時間的パターンを認識しやすくなった」と効果を検証しています(降雨予測の例など)。このようにKaggle界隈では定番テクニックであり、CatBoostを用いたケースでもまず試される特徴量です。
- システムトレード・アルゴリズム取引: 為替や株式のアルゴリズム取引においても、時間帯(マーケットセッション)や曜日による傾向を捉えるため、特徴量エンジニアリングとしてsin/cosエンコーディングが使われることがあります。とくに24時間連続稼働の為替市場では、ロンドン時間・NY時間など明確な時間帯効果が知られており、それをモデルに認識させるには有用です。ただし、市場の状態は変化するため過去の周期が将来も続く保証はなく、定期的にモデルを更新して新しいデータで再学習することが大切です。
- その他の事例: エネルギー需要予測、交通量予測、気温予測など周期性の強い時系列では、サイクリックエンコーディングが高精度化に寄与した事例が多く報告されています。例えば電力消費の予測では、「曜日と時間をsin/cosでエンコードすることで季節性や日周期をうまく捉え、予測性能が向上した」という報告がありますmdpi.com。一方、人間の行動が絡むデータでは先に述べたように工夫が必要ですが、それでもまず試してみる価値のある手法として広く受け入れられています。
まとめ
サイクリックエンコーディング(sin/cos変換)は、時間に関わる特徴量の周期構造をモデルに伝える有力な手法です。特にニューラルネットや線形モデルでは、その効果は顕著で、端点同士の連続性を表現することで過学習を防ぎつつ汎化性能を高めることができますmdpi.com。一方、CatBoostのような決定木モデルでは、サイクリック特徴をそのまま使っても必ずしも性能向上しない場合もありgithub.com、カテゴリのまま扱ったり補助的なワンホット特徴を加えたりといった工夫も視野に入れる必要がありますshrmtmt.medium.comarxiv.org。金融時系列のような分野では、周期的なパターンを捉えることが精度向上の鍵になりますが、その周期は厳密なサイクルというより人為的要因で変動する部分もあります。したがって、サイクリックエンコーディングは「基本として取り入れつつも、他の特徴量やモデル設定と組み合わせて柔軟に対処する」ことが重要です。
最後に、初心者の方はまず小さな実験から試してみると理解が深まるでしょう。例えば、自分で時系列データに対しサイクリック変換の有無でCatBoostの精度を比較してみたり、sin/cos特徴を可視化してみると、その効果実感できるはずです。サイクリックエンコーディングはシンプルですが強力なテクニックなので、ぜひ時系列特徴量の処理に役立ててみてください。
参考文献・情報源: サイクリックエンコーディングの考え方と効果mdpi.commdpi.com、決定木モデルにおける扱いstackoverflow.comgithub.com、金融データへの適用事例arxiv.org、ならびにKaggleやブログでの知見nimasarang.comshrmtmt.medium.comなどを参照しました。